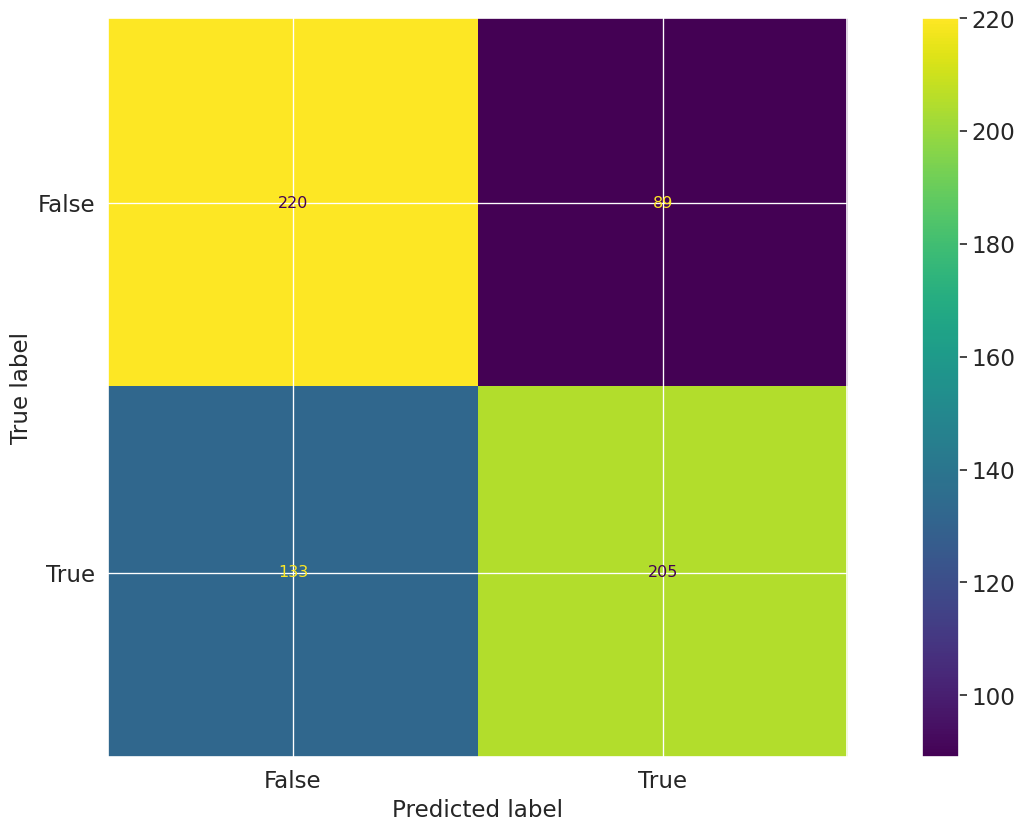
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1135: FutureWarning: 'penalty' was deprecated in version 1.8 and will be removed in 1.10. To avoid this warning, leave 'penalty' set to its default value and use 'l1_ratio' or 'C' instead. Use l1_ratio=0 instead of penalty='l2', l1_ratio=1 instead of penalty='l1', and C=np.inf instead of penalty=None.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1160: UserWarning: Inconsistent values: penalty=l1 with l1_ratio=0.0. penalty is deprecated. Please use l1_ratio only.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1135: FutureWarning: 'penalty' was deprecated in version 1.8 and will be removed in 1.10. To avoid this warning, leave 'penalty' set to its default value and use 'l1_ratio' or 'C' instead. Use l1_ratio=0 instead of penalty='l2', l1_ratio=1 instead of penalty='l1', and C=np.inf instead of penalty=None.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1160: UserWarning: Inconsistent values: penalty=l1 with l1_ratio=0.0. penalty is deprecated. Please use l1_ratio only.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1135: FutureWarning: 'penalty' was deprecated in version 1.8 and will be removed in 1.10. To avoid this warning, leave 'penalty' set to its default value and use 'l1_ratio' or 'C' instead. Use l1_ratio=0 instead of penalty='l2', l1_ratio=1 instead of penalty='l1', and C=np.inf instead of penalty=None.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1160: UserWarning: Inconsistent values: penalty=l1 with l1_ratio=0.0. penalty is deprecated. Please use l1_ratio only.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1135: FutureWarning: 'penalty' was deprecated in version 1.8 and will be removed in 1.10. To avoid this warning, leave 'penalty' set to its default value and use 'l1_ratio' or 'C' instead. Use l1_ratio=0 instead of penalty='l2', l1_ratio=1 instead of penalty='l1', and C=np.inf instead of penalty=None.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1160: UserWarning: Inconsistent values: penalty=l1 with l1_ratio=0.0. penalty is deprecated. Please use l1_ratio only.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1135: FutureWarning: 'penalty' was deprecated in version 1.8 and will be removed in 1.10. To avoid this warning, leave 'penalty' set to its default value and use 'l1_ratio' or 'C' instead. Use l1_ratio=0 instead of penalty='l2', l1_ratio=1 instead of penalty='l1', and C=np.inf instead of penalty=None.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1160: UserWarning: Inconsistent values: penalty=l1 with l1_ratio=0.0. penalty is deprecated. Please use l1_ratio only.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1135: FutureWarning: 'penalty' was deprecated in version 1.8 and will be removed in 1.10. To avoid this warning, leave 'penalty' set to its default value and use 'l1_ratio' or 'C' instead. Use l1_ratio=0 instead of penalty='l2', l1_ratio=1 instead of penalty='l1', and C=np.inf instead of penalty=None.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1135: FutureWarning: 'penalty' was deprecated in version 1.8 and will be removed in 1.10. To avoid this warning, leave 'penalty' set to its default value and use 'l1_ratio' or 'C' instead. Use l1_ratio=0 instead of penalty='l2', l1_ratio=1 instead of penalty='l1', and C=np.inf instead of penalty=None.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1135: FutureWarning: 'penalty' was deprecated in version 1.8 and will be removed in 1.10. To avoid this warning, leave 'penalty' set to its default value and use 'l1_ratio' or 'C' instead. Use l1_ratio=0 instead of penalty='l2', l1_ratio=1 instead of penalty='l1', and C=np.inf instead of penalty=None.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1135: FutureWarning: 'penalty' was deprecated in version 1.8 and will be removed in 1.10. To avoid this warning, leave 'penalty' set to its default value and use 'l1_ratio' or 'C' instead. Use l1_ratio=0 instead of penalty='l2', l1_ratio=1 instead of penalty='l1', and C=np.inf instead of penalty=None.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1135: FutureWarning: 'penalty' was deprecated in version 1.8 and will be removed in 1.10. To avoid this warning, leave 'penalty' set to its default value and use 'l1_ratio' or 'C' instead. Use l1_ratio=0 instead of penalty='l2', l1_ratio=1 instead of penalty='l1', and C=np.inf instead of penalty=None.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1135: FutureWarning: 'penalty' was deprecated in version 1.8 and will be removed in 1.10. To avoid this warning, leave 'penalty' set to its default value and use 'l1_ratio' or 'C' instead. Use l1_ratio=0 instead of penalty='l2', l1_ratio=1 instead of penalty='l1', and C=np.inf instead of penalty=None.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1160: UserWarning: Inconsistent values: penalty=l1 with l1_ratio=0.0. penalty is deprecated. Please use l1_ratio only.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1135: FutureWarning: 'penalty' was deprecated in version 1.8 and will be removed in 1.10. To avoid this warning, leave 'penalty' set to its default value and use 'l1_ratio' or 'C' instead. Use l1_ratio=0 instead of penalty='l2', l1_ratio=1 instead of penalty='l1', and C=np.inf instead of penalty=None.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1160: UserWarning: Inconsistent values: penalty=l1 with l1_ratio=0.0. penalty is deprecated. Please use l1_ratio only.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1135: FutureWarning: 'penalty' was deprecated in version 1.8 and will be removed in 1.10. To avoid this warning, leave 'penalty' set to its default value and use 'l1_ratio' or 'C' instead. Use l1_ratio=0 instead of penalty='l2', l1_ratio=1 instead of penalty='l1', and C=np.inf instead of penalty=None.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1160: UserWarning: Inconsistent values: penalty=l1 with l1_ratio=0.0. penalty is deprecated. Please use l1_ratio only.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1135: FutureWarning: 'penalty' was deprecated in version 1.8 and will be removed in 1.10. To avoid this warning, leave 'penalty' set to its default value and use 'l1_ratio' or 'C' instead. Use l1_ratio=0 instead of penalty='l2', l1_ratio=1 instead of penalty='l1', and C=np.inf instead of penalty=None.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1160: UserWarning: Inconsistent values: penalty=l1 with l1_ratio=0.0. penalty is deprecated. Please use l1_ratio only.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1135: FutureWarning: 'penalty' was deprecated in version 1.8 and will be removed in 1.10. To avoid this warning, leave 'penalty' set to its default value and use 'l1_ratio' or 'C' instead. Use l1_ratio=0 instead of penalty='l2', l1_ratio=1 instead of penalty='l1', and C=np.inf instead of penalty=None.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1160: UserWarning: Inconsistent values: penalty=l1 with l1_ratio=0.0. penalty is deprecated. Please use l1_ratio only.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1135: FutureWarning: 'penalty' was deprecated in version 1.8 and will be removed in 1.10. To avoid this warning, leave 'penalty' set to its default value and use 'l1_ratio' or 'C' instead. Use l1_ratio=0 instead of penalty='l2', l1_ratio=1 instead of penalty='l1', and C=np.inf instead of penalty=None.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1135: FutureWarning: 'penalty' was deprecated in version 1.8 and will be removed in 1.10. To avoid this warning, leave 'penalty' set to its default value and use 'l1_ratio' or 'C' instead. Use l1_ratio=0 instead of penalty='l2', l1_ratio=1 instead of penalty='l1', and C=np.inf instead of penalty=None.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1135: FutureWarning: 'penalty' was deprecated in version 1.8 and will be removed in 1.10. To avoid this warning, leave 'penalty' set to its default value and use 'l1_ratio' or 'C' instead. Use l1_ratio=0 instead of penalty='l2', l1_ratio=1 instead of penalty='l1', and C=np.inf instead of penalty=None.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1135: FutureWarning: 'penalty' was deprecated in version 1.8 and will be removed in 1.10. To avoid this warning, leave 'penalty' set to its default value and use 'l1_ratio' or 'C' instead. Use l1_ratio=0 instead of penalty='l2', l1_ratio=1 instead of penalty='l1', and C=np.inf instead of penalty=None.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1135: FutureWarning: 'penalty' was deprecated in version 1.8 and will be removed in 1.10. To avoid this warning, leave 'penalty' set to its default value and use 'l1_ratio' or 'C' instead. Use l1_ratio=0 instead of penalty='l2', l1_ratio=1 instead of penalty='l1', and C=np.inf instead of penalty=None.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1135: FutureWarning: 'penalty' was deprecated in version 1.8 and will be removed in 1.10. To avoid this warning, leave 'penalty' set to its default value and use 'l1_ratio' or 'C' instead. Use l1_ratio=0 instead of penalty='l2', l1_ratio=1 instead of penalty='l1', and C=np.inf instead of penalty=None.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1160: UserWarning: Inconsistent values: penalty=l1 with l1_ratio=0.0. penalty is deprecated. Please use l1_ratio only.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1135: FutureWarning: 'penalty' was deprecated in version 1.8 and will be removed in 1.10. To avoid this warning, leave 'penalty' set to its default value and use 'l1_ratio' or 'C' instead. Use l1_ratio=0 instead of penalty='l2', l1_ratio=1 instead of penalty='l1', and C=np.inf instead of penalty=None.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1160: UserWarning: Inconsistent values: penalty=l1 with l1_ratio=0.0. penalty is deprecated. Please use l1_ratio only.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1135: FutureWarning: 'penalty' was deprecated in version 1.8 and will be removed in 1.10. To avoid this warning, leave 'penalty' set to its default value and use 'l1_ratio' or 'C' instead. Use l1_ratio=0 instead of penalty='l2', l1_ratio=1 instead of penalty='l1', and C=np.inf instead of penalty=None.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1160: UserWarning: Inconsistent values: penalty=l1 with l1_ratio=0.0. penalty is deprecated. Please use l1_ratio only.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1135: FutureWarning: 'penalty' was deprecated in version 1.8 and will be removed in 1.10. To avoid this warning, leave 'penalty' set to its default value and use 'l1_ratio' or 'C' instead. Use l1_ratio=0 instead of penalty='l2', l1_ratio=1 instead of penalty='l1', and C=np.inf instead of penalty=None.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1160: UserWarning: Inconsistent values: penalty=l1 with l1_ratio=0.0. penalty is deprecated. Please use l1_ratio only.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1135: FutureWarning: 'penalty' was deprecated in version 1.8 and will be removed in 1.10. To avoid this warning, leave 'penalty' set to its default value and use 'l1_ratio' or 'C' instead. Use l1_ratio=0 instead of penalty='l2', l1_ratio=1 instead of penalty='l1', and C=np.inf instead of penalty=None.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1160: UserWarning: Inconsistent values: penalty=l1 with l1_ratio=0.0. penalty is deprecated. Please use l1_ratio only.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1135: FutureWarning: 'penalty' was deprecated in version 1.8 and will be removed in 1.10. To avoid this warning, leave 'penalty' set to its default value and use 'l1_ratio' or 'C' instead. Use l1_ratio=0 instead of penalty='l2', l1_ratio=1 instead of penalty='l1', and C=np.inf instead of penalty=None.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1135: FutureWarning: 'penalty' was deprecated in version 1.8 and will be removed in 1.10. To avoid this warning, leave 'penalty' set to its default value and use 'l1_ratio' or 'C' instead. Use l1_ratio=0 instead of penalty='l2', l1_ratio=1 instead of penalty='l1', and C=np.inf instead of penalty=None.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1135: FutureWarning: 'penalty' was deprecated in version 1.8 and will be removed in 1.10. To avoid this warning, leave 'penalty' set to its default value and use 'l1_ratio' or 'C' instead. Use l1_ratio=0 instead of penalty='l2', l1_ratio=1 instead of penalty='l1', and C=np.inf instead of penalty=None.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1135: FutureWarning: 'penalty' was deprecated in version 1.8 and will be removed in 1.10. To avoid this warning, leave 'penalty' set to its default value and use 'l1_ratio' or 'C' instead. Use l1_ratio=0 instead of penalty='l2', l1_ratio=1 instead of penalty='l1', and C=np.inf instead of penalty=None.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1135: FutureWarning: 'penalty' was deprecated in version 1.8 and will be removed in 1.10. To avoid this warning, leave 'penalty' set to its default value and use 'l1_ratio' or 'C' instead. Use l1_ratio=0 instead of penalty='l2', l1_ratio=1 instead of penalty='l1', and C=np.inf instead of penalty=None.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1135: FutureWarning: 'penalty' was deprecated in version 1.8 and will be removed in 1.10. To avoid this warning, leave 'penalty' set to its default value and use 'l1_ratio' or 'C' instead. Use l1_ratio=0 instead of penalty='l2', l1_ratio=1 instead of penalty='l1', and C=np.inf instead of penalty=None.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1160: UserWarning: Inconsistent values: penalty=l1 with l1_ratio=0.0. penalty is deprecated. Please use l1_ratio only.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1135: FutureWarning: 'penalty' was deprecated in version 1.8 and will be removed in 1.10. To avoid this warning, leave 'penalty' set to its default value and use 'l1_ratio' or 'C' instead. Use l1_ratio=0 instead of penalty='l2', l1_ratio=1 instead of penalty='l1', and C=np.inf instead of penalty=None.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1160: UserWarning: Inconsistent values: penalty=l1 with l1_ratio=0.0. penalty is deprecated. Please use l1_ratio only.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1135: FutureWarning: 'penalty' was deprecated in version 1.8 and will be removed in 1.10. To avoid this warning, leave 'penalty' set to its default value and use 'l1_ratio' or 'C' instead. Use l1_ratio=0 instead of penalty='l2', l1_ratio=1 instead of penalty='l1', and C=np.inf instead of penalty=None.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1160: UserWarning: Inconsistent values: penalty=l1 with l1_ratio=0.0. penalty is deprecated. Please use l1_ratio only.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1135: FutureWarning: 'penalty' was deprecated in version 1.8 and will be removed in 1.10. To avoid this warning, leave 'penalty' set to its default value and use 'l1_ratio' or 'C' instead. Use l1_ratio=0 instead of penalty='l2', l1_ratio=1 instead of penalty='l1', and C=np.inf instead of penalty=None.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1160: UserWarning: Inconsistent values: penalty=l1 with l1_ratio=0.0. penalty is deprecated. Please use l1_ratio only.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1135: FutureWarning: 'penalty' was deprecated in version 1.8 and will be removed in 1.10. To avoid this warning, leave 'penalty' set to its default value and use 'l1_ratio' or 'C' instead. Use l1_ratio=0 instead of penalty='l2', l1_ratio=1 instead of penalty='l1', and C=np.inf instead of penalty=None.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1160: UserWarning: Inconsistent values: penalty=l1 with l1_ratio=0.0. penalty is deprecated. Please use l1_ratio only.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1135: FutureWarning: 'penalty' was deprecated in version 1.8 and will be removed in 1.10. To avoid this warning, leave 'penalty' set to its default value and use 'l1_ratio' or 'C' instead. Use l1_ratio=0 instead of penalty='l2', l1_ratio=1 instead of penalty='l1', and C=np.inf instead of penalty=None.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1135: FutureWarning: 'penalty' was deprecated in version 1.8 and will be removed in 1.10. To avoid this warning, leave 'penalty' set to its default value and use 'l1_ratio' or 'C' instead. Use l1_ratio=0 instead of penalty='l2', l1_ratio=1 instead of penalty='l1', and C=np.inf instead of penalty=None.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1135: FutureWarning: 'penalty' was deprecated in version 1.8 and will be removed in 1.10. To avoid this warning, leave 'penalty' set to its default value and use 'l1_ratio' or 'C' instead. Use l1_ratio=0 instead of penalty='l2', l1_ratio=1 instead of penalty='l1', and C=np.inf instead of penalty=None.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1135: FutureWarning: 'penalty' was deprecated in version 1.8 and will be removed in 1.10. To avoid this warning, leave 'penalty' set to its default value and use 'l1_ratio' or 'C' instead. Use l1_ratio=0 instead of penalty='l2', l1_ratio=1 instead of penalty='l1', and C=np.inf instead of penalty=None.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1135: FutureWarning: 'penalty' was deprecated in version 1.8 and will be removed in 1.10. To avoid this warning, leave 'penalty' set to its default value and use 'l1_ratio' or 'C' instead. Use l1_ratio=0 instead of penalty='l2', l1_ratio=1 instead of penalty='l1', and C=np.inf instead of penalty=None.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1135: FutureWarning: 'penalty' was deprecated in version 1.8 and will be removed in 1.10. To avoid this warning, leave 'penalty' set to its default value and use 'l1_ratio' or 'C' instead. Use l1_ratio=0 instead of penalty='l2', l1_ratio=1 instead of penalty='l1', and C=np.inf instead of penalty=None.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1160: UserWarning: Inconsistent values: penalty=l1 with l1_ratio=0.0. penalty is deprecated. Please use l1_ratio only.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1135: FutureWarning: 'penalty' was deprecated in version 1.8 and will be removed in 1.10. To avoid this warning, leave 'penalty' set to its default value and use 'l1_ratio' or 'C' instead. Use l1_ratio=0 instead of penalty='l2', l1_ratio=1 instead of penalty='l1', and C=np.inf instead of penalty=None.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1160: UserWarning: Inconsistent values: penalty=l1 with l1_ratio=0.0. penalty is deprecated. Please use l1_ratio only.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1135: FutureWarning: 'penalty' was deprecated in version 1.8 and will be removed in 1.10. To avoid this warning, leave 'penalty' set to its default value and use 'l1_ratio' or 'C' instead. Use l1_ratio=0 instead of penalty='l2', l1_ratio=1 instead of penalty='l1', and C=np.inf instead of penalty=None.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1160: UserWarning: Inconsistent values: penalty=l1 with l1_ratio=0.0. penalty is deprecated. Please use l1_ratio only.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1135: FutureWarning: 'penalty' was deprecated in version 1.8 and will be removed in 1.10. To avoid this warning, leave 'penalty' set to its default value and use 'l1_ratio' or 'C' instead. Use l1_ratio=0 instead of penalty='l2', l1_ratio=1 instead of penalty='l1', and C=np.inf instead of penalty=None.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1160: UserWarning: Inconsistent values: penalty=l1 with l1_ratio=0.0. penalty is deprecated. Please use l1_ratio only.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1135: FutureWarning: 'penalty' was deprecated in version 1.8 and will be removed in 1.10. To avoid this warning, leave 'penalty' set to its default value and use 'l1_ratio' or 'C' instead. Use l1_ratio=0 instead of penalty='l2', l1_ratio=1 instead of penalty='l1', and C=np.inf instead of penalty=None.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1160: UserWarning: Inconsistent values: penalty=l1 with l1_ratio=0.0. penalty is deprecated. Please use l1_ratio only.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1135: FutureWarning: 'penalty' was deprecated in version 1.8 and will be removed in 1.10. To avoid this warning, leave 'penalty' set to its default value and use 'l1_ratio' or 'C' instead. Use l1_ratio=0 instead of penalty='l2', l1_ratio=1 instead of penalty='l1', and C=np.inf instead of penalty=None.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1135: FutureWarning: 'penalty' was deprecated in version 1.8 and will be removed in 1.10. To avoid this warning, leave 'penalty' set to its default value and use 'l1_ratio' or 'C' instead. Use l1_ratio=0 instead of penalty='l2', l1_ratio=1 instead of penalty='l1', and C=np.inf instead of penalty=None.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1135: FutureWarning: 'penalty' was deprecated in version 1.8 and will be removed in 1.10. To avoid this warning, leave 'penalty' set to its default value and use 'l1_ratio' or 'C' instead. Use l1_ratio=0 instead of penalty='l2', l1_ratio=1 instead of penalty='l1', and C=np.inf instead of penalty=None.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1135: FutureWarning: 'penalty' was deprecated in version 1.8 and will be removed in 1.10. To avoid this warning, leave 'penalty' set to its default value and use 'l1_ratio' or 'C' instead. Use l1_ratio=0 instead of penalty='l2', l1_ratio=1 instead of penalty='l1', and C=np.inf instead of penalty=None.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1135: FutureWarning: 'penalty' was deprecated in version 1.8 and will be removed in 1.10. To avoid this warning, leave 'penalty' set to its default value and use 'l1_ratio' or 'C' instead. Use l1_ratio=0 instead of penalty='l2', l1_ratio=1 instead of penalty='l1', and C=np.inf instead of penalty=None.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1135: FutureWarning: 'penalty' was deprecated in version 1.8 and will be removed in 1.10. To avoid this warning, leave 'penalty' set to its default value and use 'l1_ratio' or 'C' instead. Use l1_ratio=0 instead of penalty='l2', l1_ratio=1 instead of penalty='l1', and C=np.inf instead of penalty=None.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1160: UserWarning: Inconsistent values: penalty=l1 with l1_ratio=0.0. penalty is deprecated. Please use l1_ratio only.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1135: FutureWarning: 'penalty' was deprecated in version 1.8 and will be removed in 1.10. To avoid this warning, leave 'penalty' set to its default value and use 'l1_ratio' or 'C' instead. Use l1_ratio=0 instead of penalty='l2', l1_ratio=1 instead of penalty='l1', and C=np.inf instead of penalty=None.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1160: UserWarning: Inconsistent values: penalty=l1 with l1_ratio=0.0. penalty is deprecated. Please use l1_ratio only.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1135: FutureWarning: 'penalty' was deprecated in version 1.8 and will be removed in 1.10. To avoid this warning, leave 'penalty' set to its default value and use 'l1_ratio' or 'C' instead. Use l1_ratio=0 instead of penalty='l2', l1_ratio=1 instead of penalty='l1', and C=np.inf instead of penalty=None.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1160: UserWarning: Inconsistent values: penalty=l1 with l1_ratio=0.0. penalty is deprecated. Please use l1_ratio only.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1135: FutureWarning: 'penalty' was deprecated in version 1.8 and will be removed in 1.10. To avoid this warning, leave 'penalty' set to its default value and use 'l1_ratio' or 'C' instead. Use l1_ratio=0 instead of penalty='l2', l1_ratio=1 instead of penalty='l1', and C=np.inf instead of penalty=None.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1160: UserWarning: Inconsistent values: penalty=l1 with l1_ratio=0.0. penalty is deprecated. Please use l1_ratio only.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1135: FutureWarning: 'penalty' was deprecated in version 1.8 and will be removed in 1.10. To avoid this warning, leave 'penalty' set to its default value and use 'l1_ratio' or 'C' instead. Use l1_ratio=0 instead of penalty='l2', l1_ratio=1 instead of penalty='l1', and C=np.inf instead of penalty=None.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1160: UserWarning: Inconsistent values: penalty=l1 with l1_ratio=0.0. penalty is deprecated. Please use l1_ratio only.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1135: FutureWarning: 'penalty' was deprecated in version 1.8 and will be removed in 1.10. To avoid this warning, leave 'penalty' set to its default value and use 'l1_ratio' or 'C' instead. Use l1_ratio=0 instead of penalty='l2', l1_ratio=1 instead of penalty='l1', and C=np.inf instead of penalty=None.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1135: FutureWarning: 'penalty' was deprecated in version 1.8 and will be removed in 1.10. To avoid this warning, leave 'penalty' set to its default value and use 'l1_ratio' or 'C' instead. Use l1_ratio=0 instead of penalty='l2', l1_ratio=1 instead of penalty='l1', and C=np.inf instead of penalty=None.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1135: FutureWarning: 'penalty' was deprecated in version 1.8 and will be removed in 1.10. To avoid this warning, leave 'penalty' set to its default value and use 'l1_ratio' or 'C' instead. Use l1_ratio=0 instead of penalty='l2', l1_ratio=1 instead of penalty='l1', and C=np.inf instead of penalty=None.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1135: FutureWarning: 'penalty' was deprecated in version 1.8 and will be removed in 1.10. To avoid this warning, leave 'penalty' set to its default value and use 'l1_ratio' or 'C' instead. Use l1_ratio=0 instead of penalty='l2', l1_ratio=1 instead of penalty='l1', and C=np.inf instead of penalty=None.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1135: FutureWarning: 'penalty' was deprecated in version 1.8 and will be removed in 1.10. To avoid this warning, leave 'penalty' set to its default value and use 'l1_ratio' or 'C' instead. Use l1_ratio=0 instead of penalty='l2', l1_ratio=1 instead of penalty='l1', and C=np.inf instead of penalty=None.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1135: FutureWarning: 'penalty' was deprecated in version 1.8 and will be removed in 1.10. To avoid this warning, leave 'penalty' set to its default value and use 'l1_ratio' or 'C' instead. Use l1_ratio=0 instead of penalty='l2', l1_ratio=1 instead of penalty='l1', and C=np.inf instead of penalty=None.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1160: UserWarning: Inconsistent values: penalty=l1 with l1_ratio=0.0. penalty is deprecated. Please use l1_ratio only.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1135: FutureWarning: 'penalty' was deprecated in version 1.8 and will be removed in 1.10. To avoid this warning, leave 'penalty' set to its default value and use 'l1_ratio' or 'C' instead. Use l1_ratio=0 instead of penalty='l2', l1_ratio=1 instead of penalty='l1', and C=np.inf instead of penalty=None.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1160: UserWarning: Inconsistent values: penalty=l1 with l1_ratio=0.0. penalty is deprecated. Please use l1_ratio only.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1135: FutureWarning: 'penalty' was deprecated in version 1.8 and will be removed in 1.10. To avoid this warning, leave 'penalty' set to its default value and use 'l1_ratio' or 'C' instead. Use l1_ratio=0 instead of penalty='l2', l1_ratio=1 instead of penalty='l1', and C=np.inf instead of penalty=None.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1160: UserWarning: Inconsistent values: penalty=l1 with l1_ratio=0.0. penalty is deprecated. Please use l1_ratio only.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1135: FutureWarning: 'penalty' was deprecated in version 1.8 and will be removed in 1.10. To avoid this warning, leave 'penalty' set to its default value and use 'l1_ratio' or 'C' instead. Use l1_ratio=0 instead of penalty='l2', l1_ratio=1 instead of penalty='l1', and C=np.inf instead of penalty=None.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1160: UserWarning: Inconsistent values: penalty=l1 with l1_ratio=0.0. penalty is deprecated. Please use l1_ratio only.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1135: FutureWarning: 'penalty' was deprecated in version 1.8 and will be removed in 1.10. To avoid this warning, leave 'penalty' set to its default value and use 'l1_ratio' or 'C' instead. Use l1_ratio=0 instead of penalty='l2', l1_ratio=1 instead of penalty='l1', and C=np.inf instead of penalty=None.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1160: UserWarning: Inconsistent values: penalty=l1 with l1_ratio=0.0. penalty is deprecated. Please use l1_ratio only.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1135: FutureWarning: 'penalty' was deprecated in version 1.8 and will be removed in 1.10. To avoid this warning, leave 'penalty' set to its default value and use 'l1_ratio' or 'C' instead. Use l1_ratio=0 instead of penalty='l2', l1_ratio=1 instead of penalty='l1', and C=np.inf instead of penalty=None.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1135: FutureWarning: 'penalty' was deprecated in version 1.8 and will be removed in 1.10. To avoid this warning, leave 'penalty' set to its default value and use 'l1_ratio' or 'C' instead. Use l1_ratio=0 instead of penalty='l2', l1_ratio=1 instead of penalty='l1', and C=np.inf instead of penalty=None.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1135: FutureWarning: 'penalty' was deprecated in version 1.8 and will be removed in 1.10. To avoid this warning, leave 'penalty' set to its default value and use 'l1_ratio' or 'C' instead. Use l1_ratio=0 instead of penalty='l2', l1_ratio=1 instead of penalty='l1', and C=np.inf instead of penalty=None.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1135: FutureWarning: 'penalty' was deprecated in version 1.8 and will be removed in 1.10. To avoid this warning, leave 'penalty' set to its default value and use 'l1_ratio' or 'C' instead. Use l1_ratio=0 instead of penalty='l2', l1_ratio=1 instead of penalty='l1', and C=np.inf instead of penalty=None.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1135: FutureWarning: 'penalty' was deprecated in version 1.8 and will be removed in 1.10. To avoid this warning, leave 'penalty' set to its default value and use 'l1_ratio' or 'C' instead. Use l1_ratio=0 instead of penalty='l2', l1_ratio=1 instead of penalty='l1', and C=np.inf instead of penalty=None.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1135: FutureWarning: 'penalty' was deprecated in version 1.8 and will be removed in 1.10. To avoid this warning, leave 'penalty' set to its default value and use 'l1_ratio' or 'C' instead. Use l1_ratio=0 instead of penalty='l2', l1_ratio=1 instead of penalty='l1', and C=np.inf instead of penalty=None.
warnings.warn(
/opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:1160: UserWarning: Inconsistent values: penalty=l1 with l1_ratio=0.0. penalty is deprecated. Please use l1_ratio only.
warnings.warn(